Note on SMPL
What is SMPL
Skinned Multi-Person Linear Model, SMPL 是一个参数化的人体模型,通过线性变形和骨骼驱动的方式来表示人体形状和姿态。这一模型在2015年由 Max Planck Institute for Intelligent Systems (德国马普所)提出,在此后十年内成为广泛应用于数字人、虚拟现实、动画制作等领域的标准人体模型。
- Skinned (蒙皮):表面形状(称之为蒙皮 / skin / shape)用3D Mesh 来表示(Vertices x 6890, Faces x 13776),定点和面是拓扑有序的,并且所有模型的拓扑结构是相同的,由同样有序的输入参数(骨骼旋转角、形状参数)来驱动。
- Linear (线性变形):解耦的形状参数(Shape)和姿态参数(Pose)作为输入,线性变换蒙皮的顶点和骨骼,通过大量人体数据训练得到这些线性变换变换矩阵,从而生成不同的姿态和形状。
参数化模型指的就是这种通过少量参数去映射复杂状态的模型。SMPL 这里的参数就是形状和姿态参数,输出模型是一个 3D Mesh。但从这里也可以看出参数通常都是具有一致(有序)性的:SMPL 的输入输出都是维度和拓扑结构一致的向量和矩阵。 那么从这个意义上,nerf 是参数化模型。但 3DGS 呢?高斯球并不是事先定义好的,而是在迭代 ssim_loss 中一边 backward 一边自适应剪枝出来的 –> scene-variant。所以 3DGS 应该是非参数化。
Model Formulation
Linear Blend Skinning (LBS)
参数化模型是靠什么变换不同姿势的?和实际的人体一样,在表面蒙皮内部还有关节(Joints)连成的骨骼(Skeleton),它们驱动了附着在骨骼上的肌肉和皮肤的变形。只要做出 3D Mesh,然后手动把蒙皮顶点绑定在骨骼和关节上,蒙皮就可以随着和它绑定的骨骼和关节的变换而变形,比如手部的蒙皮绑定在手腕上,做一样的世界坐标变换就行了。而 SMPL 没有手动绑定蒙皮顶点,而是通过数据驱动的方式来学习骨骼和关节对蒙皮顶点的影响程度(权重),从而实现由全体姿态参数驱动的蒙皮变形。
SMPL 模型的驱动主要依靠 Linear Blend Skinning (LBS) ,即线性混合蒙皮:通过所有骨骼关键点的姿态(Pose)变换线性加权,驱动蒙皮顶点的坐标变换。这需要两个步骤:一是定义关节的旋转变换,并使蒙皮顶点随着关节变换而相应变换;二是定义所有关节(骨骼)对所有蒙皮顶点的影响程度(权重),使蒙皮顶点的变换最终是所有关节变换的加权平均,然后我们用数据学这个权重矩阵。
LBS 部分并不是 SMPL 模型提出的,而是属于一类通用的线性蒙皮方法(文章里推公式用的是最简单的 LBS, 还有 另外的 Blend Skinning 方式,如 DQBS 等)。但 SMPL-LBS 通过数据驱动的方式来学习权重矩阵 \(\mathbf{W}\),使得模型可以适应不同的人体形状和姿态。
SMPL 模型定义了 24 个关节(Joints),每个关节都对应唯一的骨骼,使得这个关节是骨骼的末端。包括第 0 个根节点(Root Joint),所有关节对应的骨骼的旋转变换都由 \(\mathbf{R}^3\) 的轴-角旋转表示,即 \(pose \ \vec{\theta} = [ \vec{\omega}_0, \vec{\omega}_1, \ldots, \vec{\omega}_{23}]\) ,其中 \(\vec{\omega}_i \in \mathbb{R}^3\) 的方向表示关节的旋转轴,模长表示旋转角度。每个关节的变换矩阵 \(\mathbf{R}_i\) 可以通过 Rodrigues’ rotation formula 计算得到: \[\exp \left(\vec{\omega}_{j}\right)=\mathcal{I}+\widehat{\bar{\omega}}_{j} \sin \left(\left\|\vec{\omega}_{j}\right\|\right)+\widehat{\bar{\omega}}_{j}^{2} \cos \left(\left\|\vec{\omega}_{j}\right\|\right)\]
其中 \(\bar{\omega}_{j} = \frac{\vec{\omega}_{j}}{\|\vec{\omega}_{j}\|}\) 是单位向量,\(\widehat{\bar{\omega}}_{j}\) 是 \(\bar{\omega}_{j}\) 的反对称矩阵。
对于第 \(k\) 个关节,\(A(k)\) 是其关节树的父节点有序集,则其世界坐标系下旋转变换矩阵(从 3x3 到 4x4,对应齐次坐标)为:
\[ G_{k}(\vec{\theta}, \mathbf{J})=\prod_{j \in A(k)}\left[\begin{array}{c|c}\exp \left(\vec{\omega}_{j}\right) & \mathbf{j}_{j} \\\hline \overrightarrow{0} & 1\end{array}\right] \]
其中 \(\mathbf{j}_{j} \in \mathbb{R}^3\) 是父关节(骨骼的开端)在静息状态(rest pose / zero pose)的世界坐标。
相对于静息状态的变换矩阵为: \[ G'_k(\vec{\theta}, \mathbf{J}) = G_k(\vec{\theta}, \mathbf{J}) G_k(\vec{\theta}^*, \mathbf{J})^{-1} \]
再引入权重矩阵 \(\mathbf{W} \in \mathbb{R}^{3N \times 4K}\) ,其中 \(N\) 是蒙皮顶点数,\(K\) 是关节数。每个蒙皮顶点(齐次坐标)的变换为: \[ \bar{t}'_i = \sum_{k=1}^{K} w_{k,i} G'_k(\vec{\theta}, \mathbf{J}) \bar{t}_i \] 这里就相当于对每一个蒙皮顶点 \(i\) ,先计算它受每一个关节 \(k\) 牵引的移动距离,再按照这些关节的实际贡献(权重 \(w_{k,i}\))进行加权平均,得到最终的位置 \(\bar{t}'_i\)。这两部分就是 LBS 的核心。
仅用 LBS 有什么问题?注意,这里 \(W\) 矩阵是通过统计数据学习到 骨骼的旋转变换 对蒙皮每个顶点的影响程度,表征的是一种全局的线性变换。最极端的情况,如果只有一个骨骼(相当于一个末端节点和一个根节点),若根节点不动,比如手腕的 local 变换(只有手腕作为末端节点对应的一个骨骼),这时无论手腕怎么转动,只有它一个 \(w\) 起作用,也就是所有点云的变换都是一样的,这很显然与手腕处真实的情况不符,即转动手腕时会有皮肤和肌肉的凸起。这种因为 LBS 的全局线性变换引起的关节附近的皮肤变形不符合实际情况, 会导致如下图所示的僵硬形变,称为 伪影 Artifacts。SMPL 通过引入 Pose Blend Shapes,在蒙皮点云附近添加了局部的偏移量 \(\Delta t_i\),来修正这种伪影。

Shape Blend Shapes
SMPL 模型用形状参数 \(\beta\) 来表示人体的形状,\(\beta\) 是对人体形状的 PCA 分解后的主成分向量。
模型定义一个形状偏移矩阵 \(\mathbf{S} \in \mathbb{R}^{3N \times |\beta|}\),在训练过程中学习得到。蒙皮顶点的形状偏移向量 \(B_S(\vec{\beta}; S) \in \mathbb{R}^{3N}\) 为: \[B_S(\vec{\beta}; S) = \sum_{n=1}^{|\vec{\beta}|} \beta_n S_n\]
Joint Regression
SMPL 模型还定义了一个关节回归矩阵 \(\mathbf{J} \in \mathbb{R}^{3K \times 3N}\),用于将蒙皮顶点的坐标线性变换到关节坐标系下。这个矩阵也是通过数据学习得到的。
由于关节的空间位置也和人的体型相关,在这里还有对 \(J\) 的形状偏移: \[J(\vec{\beta}; \mathcal{J}, \overline{\mathbf{T}}, S) = \mathcal{J}(\overline{\mathbf{T}} + B_S(\vec{\beta}; S))\]
Pose Blend Shapes
SMPL 模型用姿态参数 \(\theta\) 来表示人体的姿态,\(\theta\) 由轴-角旋转向量 \(\vec{\omega}\) 组成。
姿态偏移矩阵 \(\mathbf{P} \in \mathbb{R}^{3N \times 9K}\),在静息状态下输入 \(\vec{\theta}\) 对应旋转阵,得到对应姿态的偏移向量 \(B_P(\vec{\theta}; P) \in \mathbb{R}^{3N}\): \[B_P(\vec{\theta}; P) = \sum_{n=1}^{9K} (R_n(\vec{\theta}) - R_n(\vec{\theta}^*)) P_n\]
Pose Blend Shapes 与 LBS 对比:

Final Model
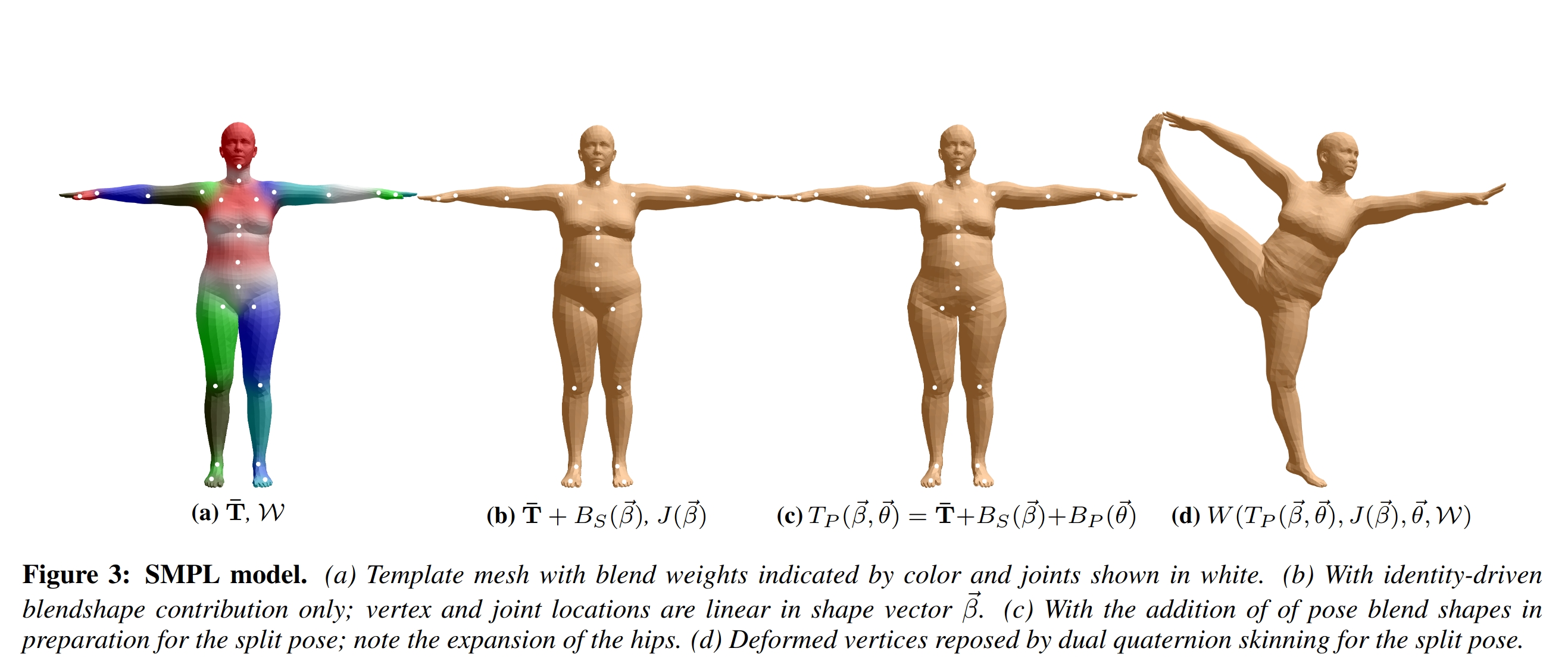
如上图所示,SMPL 模型的计算分以下几步:
- Shape Blend Shapes:计算形状偏移 \(B_S(\vec{\beta}; S)\),得到形状偏移向量;计算形状相关的关节位置 \(J(\vec{\beta}; \mathcal{J})\)。
- Pose Blend Shapes:计算姿态偏移 \(B_P(\vec{\theta}; P)\),得到姿态偏移向量。
- Linear Blend Skinning:用 Blend Shapes Correction 后的静息蒙皮顶点坐标计算每个蒙皮顶点的变换 \(\bar{t}'_i\),得到最终的蒙皮顶点坐标。
最终的蒙皮顶点坐标 \({t}'_i\) 公式为:

